Koonuslõike geomeetria

Koonuslõige, mida geomeetrias nimetatakse ka koonuseks, on mis tahes kõver, mis tekib tasapinna ja parema ümmarguse koonuse ristmikul. Sõltuvalt tasapinna nurgast koonuse suhtes on ristmik ring, ellips, hüperbool või parabool. Spetsiaalsed (degenereerunud) ristumisjuhtumid tekivad siis, kui lennuk läbib ainult tipu (tekitades ühe punkti) või läbi tipu ja koonuse teise punkti (tekitades ühe sirgjoone või kaks ristuvat sirget). Vaadake joonist.

projektiivne geomeetria: Projektiivsed koonilised lõigud

Koonuslõikeid ( s) võib käsitada parema ümmarguse koonuse tasapinnaliste lõikudena (vt joonis). Arvestades

Koonuslõikude põhikirjeldusi, kuid mitte nimesid, saab jälgida Menaechmusele (õitsenud umbes 350 bc), mis on nii Platoni kui ka Cniduse Eudoxuse õpilane. Perga Apollonius (umbes 262–190 bc), tuntud kui „Suur geomeeter“, andis koonilistele lõikudele oma nimed ja määratles esimesena hüperbooli kaks haru (mis eeldavad topeltkoonust). Apolloniuse kaheksaköiteline traktaat kooniliste lõikude kohta Conics on üks antiikmaailma suurimaid teaduslikke töid.

Analüütiline määratlus

Koonuseid võib kirjeldada ka tasapinnaliste kõveratena, mis on punkti liikumisteed (lookused) liikudes nii, et selle vahemaa suhe fikseeritud punktist (fookus) ja kaugus fikseeritud joonest (directrix) on konstant, mida nimetatakse kõvera ekstsentrilisus. Kui ekstsentrilisus on null, on kõver ring; kui see on võrdne ühega, siis parabool; kui vähem kui üks, ellips; ja kui suurem kui üks, siis hüperbool. Vaadake joonist.

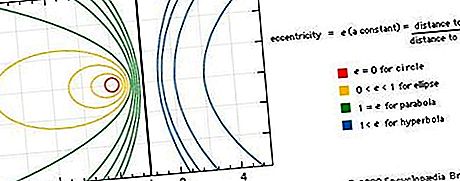
Iga koonuslõige vastab vormi Ax ² + teise astme polünoomi võrrandi graafikule + By ² + 2Cxy + 2Dx + 2Ey + F = 0, kus x ja y on muutujad ning A, B, C, D, E ja F on koefitsiendid, mis sõltuvad konkreetsest koonusest. Sobiva koordinaattelgede valiku abil saab iga koonuse võrrandi redutseerida kolmeks lihtsaks r-vormiks: ^{x 2 / _{a 2} + y 2 / _{b 2} = 1, x 2 / _{a 2} - y 2 / _{b 2} = 1 või y 2 = 2 px, vastavalt vastavalt ellipsile, hüperboole ja paraboole. (Ellips, kus a = b on tegelikult ring.) Koordinaatsüsteemide laialdane kasutamine geomeetriliste kõverate algebraliseks analüüsiks sai alguse René Descartes'ist (1596–1650). Vaadake geomeetria ajalugu: Descartes'i geomeetria.}

Kreeka päritolu

Kooniliste lõikude varases ajaloos on ühendatud kuubi kahekordistamise probleem. Küreeni Eratosthenese (umbes 276–190 bc) sõnul konsulteerisid Delose inimesed katku (c. 430 bc) katkestamiseks Apollo oraaklitega ja kästi ehitada Apollole uus altar, mis oleks kahekordne vana altari maht. ja sama kuubikujuline. Hämmingus pidasid Delians Platoniga nõu, väites, et “oraakel ei tähendanud mitte seda, et jumal tahaks kahekordse suurusega altarit, vaid ta soovis neile ülesande seadmisel häbistada kreeklasi nende hoolimatusest matemaatika ja põlguse vastu. geomeetria jaoks. ” Chiose Hippokrates (umbes 470–410 bc) avastas kõigepealt, et Deliani probleemi saab taandada kahe keskmise proportsiooni leidmisele a ja 2a vahel (vastavate altarite ruumalad) - see tähendab, määrates x ja y selliselt, et a: x = x: y = y: 2a. See võrdub lahendamisel samaaegselt tahes kaks võrrandid x ² = ay, y ² = 2Ax ja xy = 2a ², mis vastavad kahele parabolisella ja hüperbooli võrra. Hiljem näitas Archimedes (umbes 290–211 bc), kuidas kasutada koonilisi sektsioone kera jagamiseks kaheks antud suhtega segmendiks.

Düklid (umbes 200 bc) näitasid geomeetriliselt, et fookuses on näiteks päikesekiirguse kiired, mis on paralleelsed pöörde paraboloidi teljega (toodetud parabooli pööramisel ümber oma sümmeetriatelje). Väidetavalt kasutas Archimedes seda vara vaenlase laevade tule süütamiseks. Ellipsi fookusomadusi nimetas Constantinoopoli Hagia Sophia katedraali üks arhitekte Tralles Anthemius Trallesist (valminud kuulutuses 537) vahendina, mis tagaks, et altar võiks kogu päeva päikesevalguse käes olla.