Diferentsiaalvõrrand, matemaatiline avaldus, mis sisaldab ühte või mitut tuletist - see tähendab termineid, mis tähistavad pidevalt muutuvate suuruste muutumise kiirust. Diferentsiaalvõrrandid on teaduses ja inseneriteaduses, aga ka paljudes teistes kvantitatiivse uurimise valdkondades väga levinud, sest muutusi läbivate süsteemide puhul saab vahetult jälgida ja mõõta nende muutuste kiirust. Diferentsiaalvõrrandi lahendus on üldiselt võrrand, mis väljendab ühe muutuja funktsionaalset sõltuvust ühest või mitmest teisest; tavaliselt sisaldab see konstantseid termineid, mida algses diferentsiaalvõrrandis ei esine. Teine viis selle ütlemiseks on see, et diferentsiaalvõrrandi lahendus loob funktsiooni, mida saab kasutada algse süsteemi käitumise ennustamiseks, vähemalt teatud piirangute piires.

analüüs: Newton ja diferentsiaalvõrrandid
analüüsi rakendamine on diferentsiaalvõrrandid, mis seovad erinevate koguste muutumiskiirusi nende hetkeväärtustega,
Diferentsiaalvõrrandid jagunevad mitmeks suureks kategooriaks ja need jagunevad omakorda paljudeks alamkategooriateks. Kõige olulisemad kategooriad on tavalised diferentsiaalvõrrandid ja osalised diferentsiaalvõrrandid. Kui võrrandis sisalduv funktsioon sõltub ainult ühest muutujast, on selle tuletised tavalised tuletised ja diferentsiaalvõrrand klassifitseeritakse tavalise diferentsiaalvõrrandina. Teisest küljest, kui funktsioon sõltub mitmest sõltumatust muutujast, nii et selle tuletised on osalised tuletised, klassifitseeritakse diferentsiaalvõrrand osalise diferentsiaalvõrrandina. Järgnevad on näited tavalistest diferentsiaalvõrranditest:
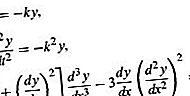
Nendes tähistab y funktsiooni ja kas t või x on sõltumatu muutuja. Sümbolid k ja m tähistavad siin konkreetseid konstante.
Olenemata tüübist, öeldakse, et diferentsiaalvõrrand on n-nda järgu, kui see hõlmab n-astme tuletist, kuid mitte ühtegi sellest kõrgemat järku tuletist. Võrrand on näide teise astme osalisest diferentsiaalvõrrandist. Tavaliste ja osaliste diferentsiaalvõrrandite teooriad on selgelt erinevad ja sel põhjusel käsitletakse kahte kategooriat eraldi.
Ühe diferentsiaalvõrrandi asemel võib uuringu objektiks olla selliste võrrandite samaaegne süsteem. Dünaamika seaduste sõnastamine viib selliste süsteemideni sageli. Mitmel juhul on n-nda astme üksikdiferentsiaal võrdselt asendatav n-n üheaegsete võrrandite süsteemiga, millest igaüks on esimeses järjekorras, nii et lineaarse algebrani meetodeid saab rakendada.
Tavaline diferentsiaalvõrrand, kus funktsiooni ja sõltumatut muutujat tähistatakse näiteks y-ga ja x, on tegelikult kaudne kokkuvõte y-funktsiooni x funktsioonist. Need omadused oleksid eeldatavasti analüüsi jaoks hõlpsamini kättesaadavad, kui saaks koostada selge y valem. Sellist valemit või vähemalt diferentsiaalvõrrandist tuletatavat valemit xides ja y-s (ilma tuletisteta), nimetatakse diferentsiaalvõrrandi lahendiks. Protsessi, mis tuleneb lahendusest võrrandist algebra ja arvutuse abil, nimetatakse võrrandi lahendamiseks või integreerimiseks. Tuleb siiski märkida, et diferentsiaalvõrrandid, mida saab selgesõnaliselt lahendada, moodustavad vaid väikese vähemuse. Seega tuleb enamikku funktsioone uurida kaudsete meetoditega. Isegi selle olemasolu tuleb tõestada, kui puudub võimalus seda kontrollimiseks toota. Praktikas kasutatakse arvuliste analüüside meetodeid, kaasates arvuteid, et saada kasulikke ligikaudseid lahendusi.