Tensoanalüüs, matemaatika haru, mis on seotud suhete või seadustega, mis jäävad kehtima sõltumata koguste täpsustamiseks kasutatavast koordinaatsüsteemist. Selliseid suhteid nimetatakse kovariantseteks. Tenorid leiutati vektorite laiendusena, et vormistada matemaatiliste kollektorite uurimisel tekkivate geomeetriliste üksuste manipuleerimine.
Vektor on entiteet, millel on nii suurus kui ka suund; see on esindatav noolejoonise abil ja see ühendab sarnaste üksustega vastavalt rööpküliku seadusele. Selle seaduse tõttu on vektoril komponendid - iga koordinaatsüsteemi jaoks erinev komplekt. Koordinaatsüsteemi muutmisel muutuvad vektori komponendid vastavalt rööpküliku seadusest tuletatavale teisenduse matemaatilisele seadusele. Sellel komponentide ümberkujundamise seadusel on kaks olulist omadust. Esiteks on pärast muudatuste jada, mis lõpeb algses koordinaatsüsteemis, vektori komponendid samad, mis alguses. Teiseks, vektorite vahelised suhted - näiteks kolm vektorit U, V, W, nii et 2U + 5V = 4W - esinevad komponentides sõltumata koordinaatsüsteemist.
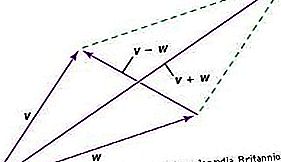
Seetõttu võib vektorit käsitada üksusena, millel on n-mõõtmelises ruumis n komponenti, mis muunduvad vastavalt spetsiifilisele muundamise seadusele, millel on ülaltoodud omadused. Vektor ise on koordinaatidest sõltumatu objektiivne entiteet, kuid seda käsitletakse komponentide osas, kus kõik koordinaatsüsteemid on võrdsetel alustel.
Piltlikku pilti nõudmata määratletakse tenor kui objektiivne üksus, mille komponendid muutuvad vastavalt transformatsiooniseadusele, mis on vektoriaalse teisenduse seaduse üldistus, kuid millel on selle seaduse kaks peamist omadust. Mugavuse huvides nummerdatakse koordinaadid tavaliselt vahemikus 1 kuni n ja tensori iga komponenti tähistatakse tähega, millel on üla- ja alaindeksid, millest igaüks võtab iseseisvalt väärtused 1 kuni n. Seega oleks komponentide T ab c esindatud tenoril n 3 komponenti, kui a, b ja c väärtus oleks vahemikus 1 kuni n. Skalaarid ja vektorid kujutavad endast tenoreid erijuhtudel: esimesel on koordinaatide süsteemi kohta ainult üks komponent ja teisel n. Mis tahes lineaarsed suhted tensorkomponentide vahel, näiteks7R a bcd + 2S a bcd - 3T a bcd = 0, kui need kehtivad ühes koordinaatsüsteemis, kehtivad kõigis ja esindavad seega suhet, mis on objektiivne ja koordinaatsüsteemidest sõltumatu, vaatamata puudub piltlik esitus.
Erilist huvi pakuvad kaks tenorit, mida nimetatakse metriliseks tensoriks ja kumeruse tenoriks. Meetrilist tenorit kasutatakse näiteks vektorikomponentide teisendamiseks vektorite suurusjärkudeks. Lihtsuse huvides kaaluge kahemõõtmelist juhtumit lihtsate risti asetsevate koordinaatidega. Olgu vektoril V komponendid V 1, V 2. Siis parempoolsele kolmnurgale OAP rakendatud Pythagorase teoreemi järgi antakse V suuruse ruut väärtuseksOP 2 = (V 1) 2 + (V 2) 2.

Selles võrrandis on peidetud meetriline tensor. See on peidetud, kuna see koosneb siin 0-st ja 1-st, mida pole sisse kirjutatud. Kui võrrand kirjutatakse ümber kujulOP 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, näib, et meetrilise tensiuri kõik komponendid (1, 0, 0, 1). Kui kasutatakse kaldus koordinaate, on OP 2 valem üldisem vormOP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, kogused g 11, g 12, g 21, g 22 on meetrilise tenori uued komponendid.
Meetrilisest tenorist on võimalik konstrueerida keeruline tendents, mida nimetatakse kõveruse tenoriks ja mis tähistab n-mõõtmelise ruumi, mille juurde see kuulub, sisemise kõveruse erinevaid aspekte.
Tensoritel on geomeetrias ja füüsikas palju rakendusi. Oma üldise relatiivsusteooria loomisel väitis Albert Einstein, et füüsikaseadused peavad olema ühesugused sõltumata sellest, millist koordinaatsüsteemi kasutatakse. See pani ta neid seadusi tensovõrrandite abil väljendama. Tema spetsiaalsest relatiivsusteooriast oli juba teada, et aeg ja ruum on üksteisega nii tihedalt seotud, et moodustavad jagamatu neljamõõtmelise ruumi-aja. Einstein postuleeris, et gravitatsiooni peaks esindama üksnes neljamõõtmelise ruumiaja meetriline tenor. Gravitatsiooni relativistliku seaduse väljendamiseks olid tal ehitusplokkidena mõõdetud tenor ja sellest moodustatud kõverus tenor. Kui ta otsustas piirduda nende ehitusplokkidega, viis nende väga nõrkus ta põhiliselt ainulaadse gravitatsiooniseaduse tensovõrrandi juurde, milles gravitatsioon ei tekkinud mitte jõuna, vaid ruumi-aja kumeruse ilminguna.
Kui tenoreid oli varem uuritud, tekitas Einsteini üldise relatiivsusteooria edu just matemaatikute ja füüsikute praegune laialdane huvi tenorite ja nende rakenduste vastu.